一文深入了解 DEX 套利和数学优化
注:原文作者是 EVM & MEV 研究者 noxx。
如果你是一名 MEV 学者,那了解如何最大化套利利润,是你应该感兴趣的事。
幸运的是,这就是我们今天要深入研究的话题。
迄今为止,区块链上最大的 MEV 形式就是套利。这个概念很简单,找到给定 token 在交易所之间的价差,执行交易,然后赚取一些利润,并在这个过程中抹平交易所之间的 token 价差。
虽然这个概念很简单,但要在大量交易所和代币中找到最高收益的套利,可能是很困难的。
Flashbots MEV 浏览器:DEX 的 MEV 及技术
在找到最佳套利时,你正在与区块链的区块时间赛跑,并且会有很多活动部分。比如交易存储池 mempool 中的新交易、中心化交易所的参考价格变化等。
幸运的是,我们发现这种最优套利对 Uniswap、Sushiswap、Balancer 等恒定函数做市商 (CFMM) 来说是一个“凸优化”问题。
这也是本文的主题,我们可以有效地解决套利问题,使其达到全局最优。
或者简单地说,我们有一个公式,可以有效地找到在一组 CFMM 中最大化套利利润的交易集。
数学优化
凸优化是数学优化的一个子领域。如果我们想要了解凸优化,一个很好的起点是获得对数学优化的高层次理解。
数学优化是根据某一标准,从一组可用备选方案中选择出最佳元素。
那么这实际上意味着什么?让我们关注最常见的用例,即在处理最小/最大问题时使用数学优化。
最小/最大问题是在给定某个“目标函数”的输入值上的一些“约束”的情况下,最小化或最大化该函数的问题。
请注意,约束可以是不等式约束(x^2+y^2>=1)或等式约束(x ^2+y ^2=1)。
例如,给定一笔预算,从超市购买尽可能多的水果,而每种水果都有不同的价格。我们的约束条件可能是,我们只能购买不超过 5 个香蕉(b <= 5 不等式约束),并且我们必须只购买一个橙子(o = 1 等式约束)。
现在让我们看一个更复杂的示例,以及用于表示问题的数学符号。我还将提供另一种方式来查看它,这对于有编程背景的人来说可能会更直观。
约束优化示例
要求你最大化目标函数 f(x,y),其中,
f ( x, y ) = x^2 * y
约束为
x^2 + y^2 = 1
让我们从这个约束开始,它为我们提供了一组可行的 x 值和 y 值。
例如,当 x =1 并且 y = 1,x^2 + y^2 = 2(不等于 1),因此,它不满足约束,并且不是有效的 x,y 位置。
当 x=0.70710678118 和 y=0.70 71067818 时,x^2+y^2=1,因此,这些 x、y 坐标确实满足约束,并且有效。
这个相同的对象函数和约束可以用 python 中的函数形式表示。我们的目标是最大化函数所返回的值。
目标函数定义为 python 函数
函数 objective_function(x,y)并等价于 f(x,y)。对于这个约束,如果不满足,我提出了一个异常,而不是使用指标/惩罚函数。
可以使用 3 个轴以图形方式查看此问题,一个用于 x,一个用于 y,一个用于返回结果 f (x, y)。
约束优化介绍
上面是一张代表这个问题的 3 维图。红圈内代表所有满足约束(x^2 + y^2 = 1)的 x,y 坐标。
可视化此图的另一种方法,是想象使用粉笔在大型操场的地板上绘制 x 和 y 轴。
约束优化介绍
给定 x, y 坐标,我们可以走到操场上的那个位置,在那个位置,一个值 f ( x, y ) 将返回给我们。
返回值是我们试图最大化的目标函数。它的值将表示地板上方或下方的某个高度。因此,地面以上/以下的高度代表我们的第三轴 f (x,y)。
如果我们能够根据返回的 f (x,y),将漂浮的网球放置在地面上方/下方,我们就可以绘制出三维图形。
我们只需在操场上走动,注意 x 和 y 位置,然后将我们的网球放在地面上方或下方的某个点。
如果在每个坐标上完成,这个浮动网球网络将与我们在上图中看到的三维图相匹配。
然后可以将最大化问题视为给定一组放置在地面上方/下方的所有操场坐标 (x, y) 的网球,其中 x^2+y^2=1 找到地面上方最高的网球。
本示例的目的是向我们展示如何构建优化问题。
我们有一些目标函数,这是我们想要最小化/最大化的东西,还有一组约束。当我们观察真实世界的套利时,这一点的重要性将变得显而易见。
这就是本文其余部分所需的全部上下文。但如果你有兴趣了解更多有关此特定问题的信息,则可以使用一组视频来描述该解决方案。最后,请随时返回并浏览它们,以帮助你理解。
现在让我们继续讨论针对 CFMM 套利的优化以及凸优化。
凸优化
首先,让我们先看看是什么让我们的 CFMM 套利优化问题变凸。我们将处理很多我们已经遇到的问题,即目标函数和约束。
目标函数必须是凸的。
等式函数可以是线性的,你可能想知道为什么等式函数可以线性,我们将在 [3] 中看到解释。
线性等式函数可以转换为 2 个不等式函数,如果等式函数是线性的,我们知道相关的不等式函数将是凸的(如果你想了解原因,请参见此处)。
不等式函数必须是凸的。
所以我们已经确定,我们需要目标函数和不等式约束是凸的,但什么决定了函数是否是凸的。
凸函数
让我们看一下定义。
在数学中,如果函数图上任意两点之间的线段位于两点之间的图上方,则将实值函数称为凸函数。
下图将有助于阐明这意味着什么。
凸函数与非凸函数
我们可以在第二张和第三张图中看到,我们能够在图下方的 2 个点之间定义一条线段,表明它们是非凸的。
如果我们看一下图上的 Uniswap (x * y = k) 函数,我们可以看到它是一个凸函数。
Uniswap (x*y=k) 函数图
这也是我们需要的所有上下文,我们已经确定我们的目标函数和不等式约束对于凸优化问题必须是凸的。
还有很多关于凸优化、对偶性、拉格朗日法、内点法等方面的知识需要学习,但它们对于理解本文的其余部分来说是不必要的。
我鼓励你在完成后深入研究这些主题,你可以从下面 3 个视频开始,它们对其中一些概念进行了很好的概述。
既然我们已经确定了 CFMM 套利问题是一个凸问题,那我们就可以继续了。
CFMM 套利路由
本节将重点介绍如何将套利问题构建为凸优化问题,并通过 python 解决该问题。
我们将大量利用 2 个资源,第一个是 Theo Diamandis 关于凸优化的演讲,第二个是 Guillermo Angeris 的凸优化 GitHub repo。在看完这篇文章后,你应该看一下这两个资料,以巩固你的理解。
本文其余部分的所有代码,都可以在这个 Gist 中找到,它是 Guillermo 的 arbitrage.py 的一个分叉,并添加了一些内容。
需要注意的一点是,在这些计算过程中,我们将忽略掉 gas,以使事情变得简单。注意,Theo 在他的演讲当中确实考虑到了 gas,如果你感兴趣的话可以看看。
现在让我们开始吧。
描述问题
给定一组 CFMM(恒定函数做市商)池子,问题陈述是它们当中是否存在套利机会,如果有,哪个是最优的?
这个问题实际上是 CFMM 路由问题的一个子集。
稍后我们将看到,添加一个额外的约束,使我们能够使用这个路由问题来解决我们的套利优化。
那我们如何将这个路由问题转化为凸优化问题呢?
让我们一步一步地运行它,带你了解数学方法并将其转换为代码。
搜索空间
我们首先定义搜索空间。我们可以定义一组 token 并找到包含这些 token 的所有池子,或者我们也可以定义一个池子集合,在这种情况下,token 由数据集中的池子定义。
我们的 token 标记为 1 到“n”,CFMM 池子将标记为 1 到“m”。
token 和池子之间的连接代表 CFMM 网络,可以使用一个二分图查看。
让我们看看这个二分图,以及在 arbitrage.py 中如何定义 token 和 CFMM(注意,在代码中,我们使用 0 到 n-1 和 0 到 m-1 的标记)
二分图 + 在 arbitrage.py 中定义搜索空间
这看上去好像很复杂,但我可以向你保证,实际上它并不复杂。
1、CFMM 池子在代码中是被称为“local_indices”的数组。每个 CFMM 池子本身就是一个数组,其中数组中的项确定该池子中可用的 token。比如“m”等于 5,意思就是我们有 5 个 CFMM 池子。
2、token 在代码中是被称为“global indices”的列表 [0,1,2,3],比如“n”等于 4,是指列表中有 4 项,这个列表中的数字表示 token,即:
0 = TOKEN-0
1 = TOKEN-1
为了简单起见,我将它们标记为 TOKEN-X,但你可以想象它们映射到真实的代币,比如 ETH、DAI、SOL 等。
3、二分图显示了左侧的 CFMM 池子以及右侧的 token。如果一个池子节点包含 token,则该池子节点连接到该 token 节点。这为我们提供了正在使用的 CFMM 池子网络的完整表示。
让我们快速浏览下每个 CFMM。
CFMM 0 是一个 Balancer 池子(Balancer 池子可以容纳 2 种以上的 token)
[ 0, 1, 2, 3 ]
其中包含 token 0、1、2 和 3
CFMM 1 是一个 UniswapV2 池子
[ 0, 1 ]
其中包含 token 0 和 1
CFMM 2 是一个 UniswapV2 池子
[ 1, 2 ]
其中包含 token 1 和 2
CFMM 3 是一个 UniswapV2 池子
[ 2, 3 ]
其中包含 token 2 和 3
CFMM 4 是一个常数和池子
[ 2, 3 ]
其中包含 token 2 和 3
在这一点上,你可能会问,为什么 token 被定义为“global_Index”,而 CFMM 池子被定义为“local_indices”?让我们来看看。
全局索引 VS 局部索引
上面的命名是指适用于所有 CFMM 池子的 token 全局索引标签和适用于特定 CFMM 池子的 token 的局部索引标签。
为了给你举个例子,我们声明了以下全局索引。
0 → TOKEN-0
1 → TOKEN-1
2 → TOKEN-2
3 → TOKEN-3
如果我们看一下 CFMM-2 的局部索引,我们有。
0 → TOKEN-1
1 → TOKEN-2
这意味着可以全局或局部查看 token 的索引映射。如果我们查看全局索引 0,我们可以看到它映射到 TOKEN-0。如果我们查看 CFMM-2 的局部索引 0,可以看到它映射到 TOKEN-1,这是全局索引映射的不同 token。
局部索引可以用下面的符号定义:
下表显示了每个 CFMM 的全局索引和局部索引。
全局索引和局部索引
由于我们的全局索引和局部索引不同,我们需要有一种将局部索引转换为全局索引的方法。
最终,我们希望在所有交易完成后,看到整个 CFMM 池子网络中每个 token 的净收益/损失。这将在全局索引中查看。
为了实现从局部索引到全局索引的转换,我们使用了一组矩阵。
下面是我们示例的矩阵集。
Ai 矩阵
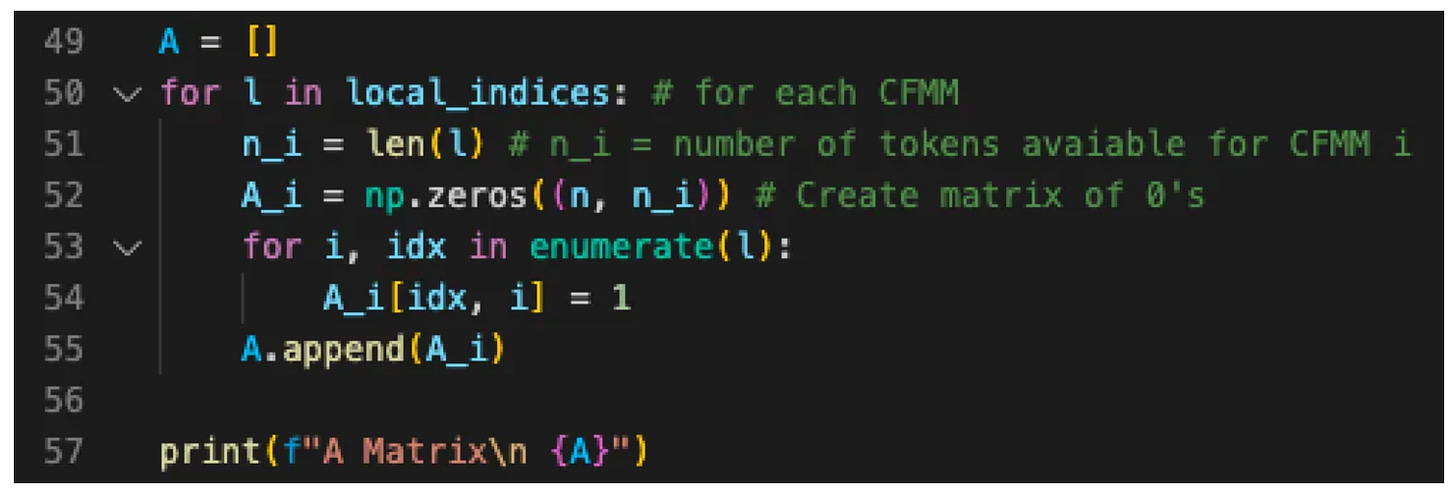
请注意,A0 映射到 CFMM-0,A1 映射到 CFMM-1 等。这些矩阵是使用以下代码生成的。
arbitrage.py 中定义的 Ai 矩阵
我们将在本文后面看到这些矩阵的作用,现在,你只需要知道它们存在,并且它们的目的是将局部索引映射到全局索引。
接下来,我们需要看看我们如何定义跨 CFMM 的交易。
交易 - Lambdas & Deltas
当和一个池子进行交易/swap 时,我们把放入池子中的金额称为“Delta”,把从池子里取出的金额称为“Lambda”。
而池子中的每个 token 都有自己的“Delta”和“Lambda”值。
例如,如果我们与 UniswapV2 的 ETH/DAI 池子进行交易,并投入 1 ETH,然后收到 2000 DAi,那么“Delta”和“Lambda”将具有以下值:
ETH
Delta = 1
Lambda = 0
DAI
Delta = 0
Lambda = 2000
交易函数
我们可以使用“Delta”和“Lambda”定义交易,并使用这些值来确保交易遵守管理池子的交易函数。
我们用希腊符号 phi φ 来定义交易函数。
交易函数符号
1、将“Delta i”和“Lambda i”与“CFMM i”进行交易
2、交易结果是将投入代币“Delta”转换为收到的代币“Lambda”
3、如果满足交易函数约束,则接受交易。交易函数 phi 接受池子储备、“Delta”、“Lambda”以及“Gamma”
(1)“Gamma”代表 1 减去 CFMM 的交易费用,这可以确保我们在将 token 添加到储备金时,考虑到从我们的“Delta”发送到协议的交易费(UniswapV2 的 0.3%)
(2)交易函数确保交易产生的新储备大于或等于旧储备的交易函数结果
让我们看看我们如何在代码中处理这个问题。
在 arbitrage.py 中定义交易和储备金
1、为每个 CFMM 池子声明储备金。在这个例子中,这些都是硬编码的,事实上,当交易发生在链上时,你会不断更新这些储备。数组 [4,4,4,4] 中的第一项表示 Balancer 池子,这意味着我们在池子中有以下内容:
TOKEN-0 的 4 个
TOKEN-1 的 4 个
TOKEN-2 的 4 个
TOKEN-3 的 4 个
2、为每个 CFMM 池子申报交易费用。交易费用定义为 1 - 实际费用。例如,UniswapV2 是 0.3% 的费用,所以我们的费用是 0.997。
3、“Deltas”和“Lambdas”是使用 cp 声明和定义的,cp 是 cvxpy 库。这个库是一个凸优化求解器。此时代码中的“Delta”和“Lambda”是抽象的,在我们要求 cvxpy 解决优化之前,它们没有真正的价值。
4、宣布了新的储备,我们可以看到它们是使用我们之前看到的等式计算的。
R= 储备
gamma =“Gamma”
D =““Delta”
L =“Lambda”
现在我们了解了如何定义每笔单独的 swap 交易,我们可以定义“净网络交易”(Net Network Trade)。
净网络交易(Net Network Trade)
“净网络交易”是网络中每个代币的 +/- 位置,指在所有交易结束时,相对于我们的起始位置。
这就是我们前面定义的“Ai”矩阵将被使用的地方。
它们允许我们对 CFMM 池子进行交易,该池由该 CFMM 上的代币在其局部索引处组成,并将其与我们的“Ai”矩阵结合以更新将代表我们的“净网络交易”的全局索引数组。
“净网络交易”由希腊字母 psi Ψ 表示。其数学符号如下所示:
净网络交易符号
上图表明 psi Ψ 是所有 CFMM 1 → m 中所有交易的总和,其中交易由“Lambda i”定义 -“Delta i”和“Ai”用于将该交易转换为其全局映射。
让我们再次深入研究代码,以 CFMM-2 为例。
矩阵的点积
1、声明 Psi。我们再次使用 cvxpy 库。@ 符号与矩阵一起使用时表示两个值的点积。我们有一个 A2 矩阵,它将局部 token 索引转换为全局 token 索引,以及(L-D)它是“Lambda”-“Delta”,即在交易过程中输入多少和输出多少。我们对 CFMM 的结果进行汇总,得出我们的“净网络交易”。
2、为不熟悉矩阵乘法的人演示点积方法。
3、此处可以看到 CFMM-2 的点生成计算结果。每行代表交易中 token 的 +/- 情况。请注意,上面的数字来自凸优化问题的 cvxpy 解决方案。
(0 * -0.224) + (0 * 0.931) = 0 = TOKEN-0
(1 * -0.224) + (0 * 0.931) = -0.224 = TOKEN-1
(0 * -0.224) + (1 * 0.931) = 0.931 = TOKEN-2
(0 * -0.224) + (0 * 0.931) = 0 = TOKEN-3
上面,我们单独研究了 CFMM-2,现在让我们看看所有 CFMM 的总和,以获得“净网络交易”矩阵。
注意,对于这个图,我们四舍五入到了小数点后 3 位,因此结果将与 Arrige.py 中的 python 输出略有不同。
arbitrage.py 中的净网络交易
每个矩阵代表在该特定 CFMM 上发生的交易,正值是接收代币,负值是投入代币。通过将所有这些交易组合在一起,我们得到了我们的“净网络交易”。
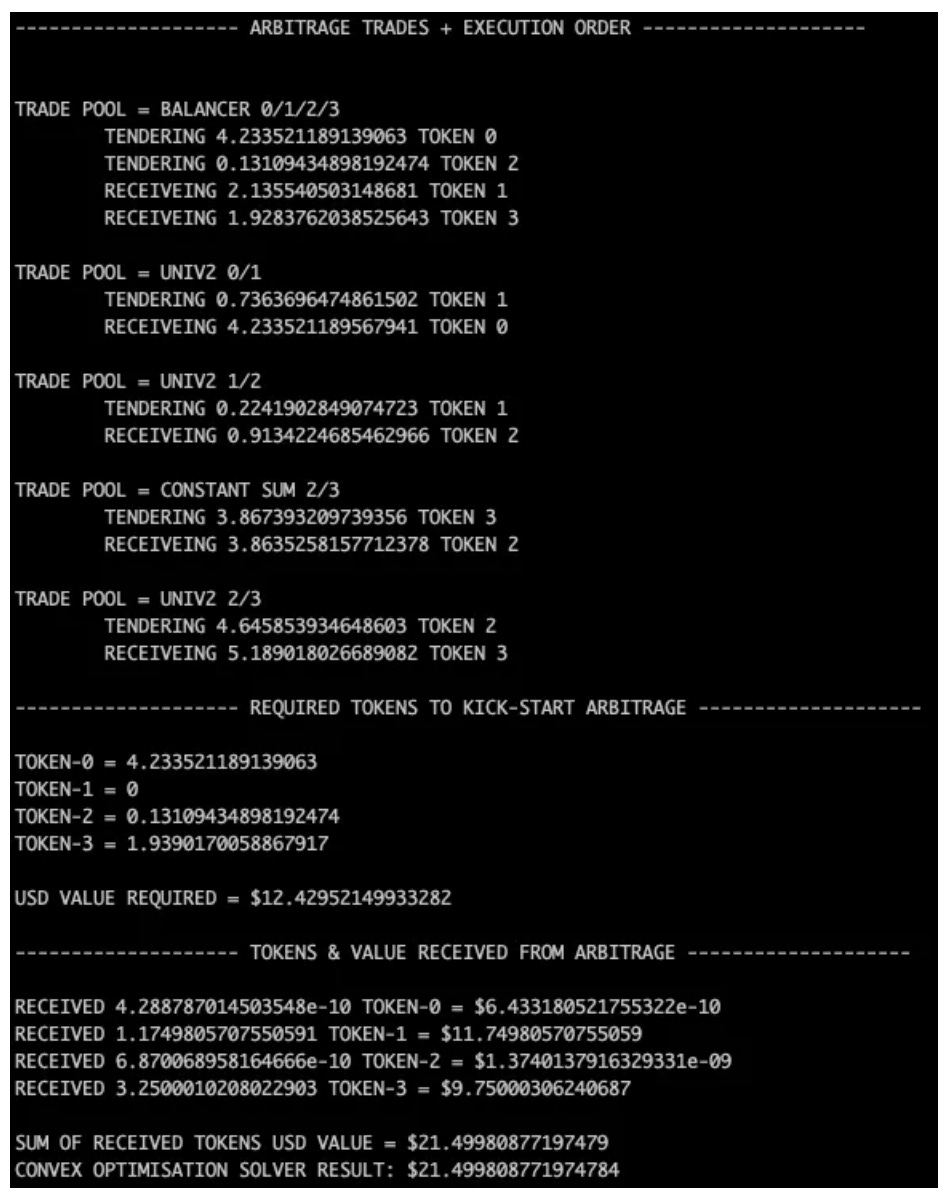
1、CFMM-0 执行交易
投入 4.234 个 TOKEN-0 以及 0.131 个 TOKEN-2
收到 2.135 个 TOKEN-1 和 1.928 个 TOKEN-3
2、CFMM-1 执行交易
投入 0.736 个 TOKEN-1
收到 4.234 个 TOKEN-0
3、CFMM-2 执行交易
投入 0.224 个 TOKEN-1
收到 0.931 个 TOKEN-2
4、CFMM-3 执行交易
投入 4.646 个 TOKEN-2
收到 5.189 个 TOKEN-3
5、CFMM-4 执行交易
投入 3.867 个 TOKEN-3
收到 3.864 个 TOKEN-4
6、净网络交易
收到 1.175 个 TOKEN-1、0.018 个 TOKEN-2 以及 3.25 个 TOKEN-3。
接下来,我们需要思考一下,我们要最大化的究竟是什么。我们的目标函数是什么?
目标函数
目标函数(有时称为效用函数)是我们想要最大化的函数。
那么,我们想要最大化的是什么?
我们希望最大化我们在所有交易结束时获得的总价值。为此,我们不能使用每个 token 的数量,因为 token 的价格不同。我们需要将 token 转换为一个通用的值单位,我们需要对数据进行归一化。
我们可以通过从具有深度流动性的外部市场获取 token 的美元价值来实现这一点。
这意味着我们的目标函数,是以美元价值最大化的“净网络交易”,让我们看看代码。
arbitrage.py 中的目标函数
1、我们定义了每个 token 的 market_value。在这里,我们使用硬编码数组,但实际上,我们会不断查询交易所端以获取最新价格。
1.50 美元是 TOKEN-0 的价格,10 美元是 TOKEN-1 的价格,等等
2、目标函数被声明为 obj,它表示我们希望最大化“market_value@psi”,正如我之前提到的那样,@在这种情况下意味着矩阵乘法。
3、这 2 个矩阵代表实际解决方案中的市场价值和 psi。所得矩阵是以美元为单位的“净网络交易”,而这正是我们试图最大化的。
如前所述,我在这里使用的值来自实际解决方案,实际上在解决凸优化之前,这些都是抽象值。
我把它们包括在内,因为我觉得看到真正的价值而不是符号有时有助于我们的理解。
请注意,有时我们可能希望最大化特定 token 的价值。如果我们只对获取 TOKEN-0 和 TOKEN-2 感兴趣,我们可以将 TOKEN-1 和 TOKEN-3 的市场价值设置为零。这种优化可以使返回的 token 1 和 token 2 价值最大化,而不是在所有 4 个 token 中实现最大化。
我们现在有了我们的目标函数,最终可以进入谜题的最后一部分,即系统的约束。
交易约束
我们在本文中设置的凸优化问题存在于 CFMM 池子的网络中。
这些池子有自己的法则来管理它们。这些法则以交易函数的形式出现,我们之前已经提到过,比如最著名的就是 Uniswap 的“x * y = k”。
深入了解每个 CFMM 的交易函数超出了本文的范围,但如果你感兴趣,请阅读这篇文章。
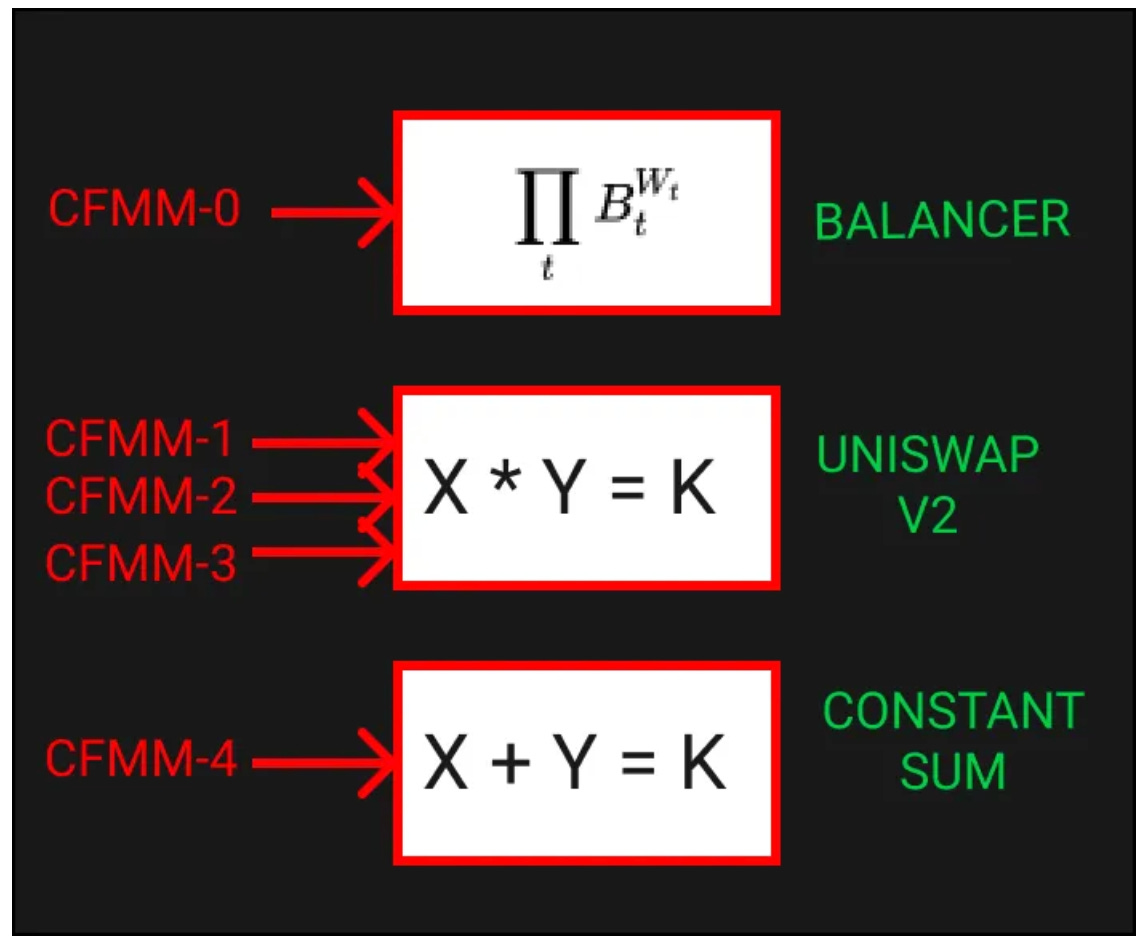
交易函数
以上是我们交易的 3 个 DEX 的交易函数,在这 3 个 DEX 中,我们在 5 个 CFMM 池子中进行套利交易。每个池子都有一个指向它使用的交易函数的箭头。
让我们看看代码中定义的这些约束。
arbitrage.py 中的约束
1、Balancer 交易函数是一个几何平均函数,它包含池子中 token 的权重,并使用 cp.geo_mean 声明,权重之和 ( [ 4, 3, 2, 1 ] ) 加起来为 1,这代表池子中的所有资产。
TOKEN-0 = 40%,TOKEN-1 = 30%,TOKEN-2 = 20%,TOKEN-3 = 10%
2、UniswapV2 也是一个几何平均 AMM,因此 cp.geo_mean 可再次用于定义 CFMM 1、2 和 3 的约束。
3、恒定和使用不同的交易函数,因此我们使用 cp.sum。
4、这不是交易函数约束,而是将我们的路由问题变成我们之前讨论的套利问题的约束。
通过声明在所有交易结束时不应该有需要投入的 token,我们将路由问题变成了套利问题。
此约束检查 psi(净网络交易)中的每个 token 是否大于或等于 0。这意味着在所有交易结束时,对于每个 token,我们要么收到该 token,要么至少不必提供任何该 token。
解决凸优化问题
现在我们有了目标函数和约束,接下来我们可以解决凸优化问题。
在 Theo 的演讲中,目标函数和约束以数学方式显示,它们有效地构成了问题的框架。
套利问题的框架
我们的目标函数,代表美元的“净网络交易”
我们对每个 CFMM 的交易约束从 1 → m
所有 CFMM 的交易金额的有效值(注意,代码中未明确定义)
套利约束,(cT)ψ 是我们的目标函数,其中(cT)是 token 的市场价值。套利约束是一个指标/惩罚函数。当 Ψ >= 0 时,它将解析为无穷大,否则解析为 0。由于 Ψ >= 0 的任何事物都会导致负无穷大,因此它确保如果不满足此条件,则不会选择排列组合(更多详细信息,请参见 Theo 的演讲)。
优化的解决方案为我们提供了净网络交易的总价值。通过查看每个 CFMM 池子的“Lambdas”和“Deltas”,我们还可以看到为了得到这个结果而进行了哪些交易。
解决 arbitrage.py 中的优化
cvxpy(cp)为解决这个问题所做的工作,会是另一篇完整的文章,因此我们不打算在这里深入讨论。如果你感兴趣,我建议从这里开始,这是 CFMMRouter.jl 的文档,这是一个在 julia 中针对这个问题编写的优化器。
对于本文的上下文,重要的是我们有一个解决凸优化问题的工具,并且我们现在知道如何以编程方式构建我们可能想问的问题。
调用 solve 后,我们将得到一个交易列表,这些交易已知是导致最佳套利的交易。我们仍然存在的一个问题是,我们不知道以什么顺序执行它们。
执行顺序
为了启动套利,第一笔交易需要一些资金(即使是来自闪电贷),因此,我们在排序交易时的目标应该是尽量减少所需的启动资金。
在这里,我们将最小化所有 token 的美元价值以启动交易。在某些情况下,你拥有一些 token x, 因此希望给该 token 加权。
交易排序的排列数是 n! (n 阶乘)其中 n 是交易次数。
在我们的例子中,我们有 5 次交易,所以我们有 5 x 4 x 3 x 2 x 1 = 120 个组合方式。
为简单起见,我们将强制交易订单以确定最佳排序。
代码相对简单,最终只是循环遍历每个排列,并记录每个 token 需要多少,同时考虑到之前交易中收到的任何 token。
你可以找到完整的 arbitrage.py 代码,然后自己动手玩。我添加了一些注释以帮助你理解。
此文件包含双向 Unicode 文本,其解释或编译方式可能与下面显示的不同。要查看,请在显示隐藏 Unicode 字符的编辑器中打开该文件。
import numpy as np
import cvxpy as cp
import itertools
# Problem data
global_indices = list(range(4))
# 0 = TOKEN-0
# 1 = TOKEN-1
# 2 = TOKEN-2
# 3 = TOKEN-3
local_indices = [
[0, 1, 2, 3], # TOKEN-0/TOKEN-1/TOKEN-2/TOKEN-3
[0, 1], # TOKEN-0/TOKEN-1
[1, 2], # TOKEN-1/TOKEN-2
[2, 3], # TOKEN-2/TOKEN-3
[2, 3] # TOKEN-2/TOKEN-3
]
reserves = list(map(np.array, [
[4, 4, 4, 4], # balancer with 4 assets in pool TOKEN-0, TOKEN-1, TOKEN-2, TOKEN-3 (4 TOKEN-0, 4 TOKEN-1, 4 TOKEN-2 & 4 TOKEN-3 IN POOL)
[10, 1], # uniswapV2 TOKEN-0/TOKEN-1 (10 TOKEN-0 & 1 TOKEN-1 IN POOL)
[1, 5], # uniswapV2 TOKEN-1/TOKEN-2 (1 TOKEN-1 & 5 TOKEN-2 IN POOL)
[40, 50], # uniswapV2 TOKEN-2/TOKEN-3 (40 TOKEN-2 & 50 TOKEN-3 IN POOL)
[10, 10] # constant_sum TOKEN-2/TOKEN-3 (10 TOKEN-2 & 10 TOKEN-3 IN POOL)
]))
fees = [
.998, # balancer fees
.997, # uniswapV2 fees
.997, # uniswapV2 fees
.997, # uniswapV2 fees
.999 # constant_sum fees
]
# "Market value" of tokens (say, in a centralized exchange)
market_value = [
1.5, # TOKEN-0
10, # TOKEN-1
2, # TOKEN-2
3 # TOKEN-3
]
# Build local-global matrices
n = len(global_indices)
m = len(local_indices)
A = []
for l in local_indices: # for each CFMM
n_i = len(l) # n_i = number of tokens avaiable for CFMM i
A_i = np.zeros((n, n_i)) # Create matrix of 0's
for i, idx in enumerate(l):
A_i[idx, i] = 1
A.append(A_i)
# Build variables
# tender delta
deltas = [cp.Variable(len(l), nonneg=True) for l in local_indices]
# receive lambda
lambdas = [cp.Variable(len(l), nonneg=True) for l in local_indices]
psi = cp.sum([A_i @ (L - D) for A_i, D, L in zip(A, deltas, lambdas)])
# Objective is to maximize "total market value" of coins out
obj = cp.Maximize(market_value @ psi) # matrix multiplication
# Reserves after trade
new_reserves = [R + gamma_i*D - L for R, gamma_i, D, L in zip(reserves, fees, deltas, lambdas)]
# Trading function constraints
cons = [
# Balancer pool with weights 4, 3, 2, 1
cp.geo_mean(new_reserves[0], p=np.array([4, 3, 2, 1])) >= cp.geo_mean(reserves[0]),
# Uniswap v2 pools
cp.geo_mean(new_reserves[1]) >= cp.geo_mean(reserves[1]),
cp.geo_mean(new_reserves[2]) >= cp.geo_mean(reserves[2]),
cp.geo_mean(new_reserves[3]) >= cp.geo_mean(reserves[3]),
# Constant sum pool
cp.sum(new_reserves[4]) >= cp.sum(reserves[4]),
new_reserves[4] >= 0,
# Arbitrage constraint
psi >= 0
]
# Set up and solve problem
prob = cp.Problem(obj, cons)
prob.solve()
# Trade Execution Ordering
current_tokens = [0, 0, 0, 0]
new_current_tokens = [0, 0, 0, 0]
tokens_required_arr = []
tokens_required_value_arr = []
pool_names = ["BALANCER 0/1/2/3", "UNIV2 0/1", "UNIV2 1/2", "UNIV2 2/3", "CONSTANT SUM 2/3"]
permutations = itertools.permutations(list(range(len(local_indices))), len(local_indices))
permutations2 = []
for permutation in permutations:
permutations2.append(permutation)
current_tokens = [0, 0, 0, 0]
new_current_tokens = [0, 0, 0, 0]
tokens_required = [0, 0, 0, 0]
for pool_id in permutation:
pool = local_indices[pool_id]
for global_token_id in pool:
local_token_index = pool.index(global_token_id)
new_current_tokens[global_token_id] = current_tokens[global_token_id] + (lambdas[pool_id].value[local_token_index] - deltas[pool_id].value[local_token_index])
if new_current_tokens[global_token_id] < 0 and new_current_tokens[global_token_id] < current_tokens[global_token_id]:
if current_tokens[global_token_id] < 0:
tokens_required[global_token_id] += (current_tokens[global_token_id] - new_current_tokens[global_token_id])
new_current_tokens[global_token_id] = 0
else:
tokens_required[global_token_id] += (-new_current_tokens[global_token_id])
new_current_tokens[global_token_id] = 0
current_tokens[global_token_id] = new_current_tokens[global_token_id]
tokens_required_value = []
for i1, i2 in zip(tokens_required, market_value):
tokens_required_value.append(i1*i2)
tokens_required_arr.append(tokens_required)
tokens_required_value_arr.append(sum(tokens_required_value))
min_value = min(tokens_required_value_arr)
min_value_index = tokens_required_value_arr.index(min_value)
print("\n-------------------- ARBITRAGE TRADES + EXECUTION ORDER --------------------\n")
for pool_id in permutations2[min_value_index]:
pool = local_indices[pool_id]
print(f"\nTRADE POOL = {pool_names[pool_id]}")
for global_token_id in pool:
local_token_index = pool.index(global_token_id)
if (lambdas[pool_id].value[local_token_index] - deltas[pool_id].value[local_token_index]) < 0:
print(f"\tTENDERING {-(lambdas[pool_id].value[local_token_index] - deltas[pool_id].value[local_token_index])} TOKEN {global_token_id}")
for global_token_id in pool:
local_token_index = pool.index(global_token_id)
if (lambdas[pool_id].value[local_token_index] - deltas[pool_id].value[local_token_index]) >= 0:
print(f"\tRECEIVEING {(lambdas[pool_id].value[local_token_index] - deltas[pool_id].value[local_token_index])} TOKEN {global_token_id}")
print("\n-------------------- REQUIRED TOKENS TO KICK-START ARBITRAGE --------------------\n")
print(f"TOKEN-0 = {tokens_required_arr[min_value_index][0]}")
print(f"TOKEN-1 = {tokens_required_arr[min_value_index][1]}")
print(f"TOKEN-2 = {tokens_required_arr[min_value_index][2]}")
print(f"TOKEN-3 = {tokens_required_arr[min_value_index][3]}")
print(f"\nUSD VALUE REQUIRED = ${min_value}")
print("\n-------------------- TOKENS & VALUE RECEIVED FROM ARBITRAGE --------------------\n")
net_network_trade_tokens = [0, 0, 0, 0]
net_network_trade_value = [0, 0, 0, 0]
for pool_id in permutations2[min_value_index]:
pool = local_indices[pool_id]
for global_token_id in pool:
local_token_index = pool.index(global_token_id)
net_network_trade_tokens[global_token_id] += lambdas[pool_id].value[local_token_index]
net_network_trade_tokens[global_token_id] -= deltas[pool_id].value[local_token_index]
for i in range(0, len(net_network_trade_tokens)):
net_network_trade_value[i] = net_network_trade_tokens[i] * market_value[i]
print(f"RECEIVED {net_network_trade_tokens[0]} TOKEN-0 = ${net_network_trade_value[0]}")
print(f"RECEIVED {net_network_trade_tokens[1]} TOKEN-1 = ${net_network_trade_value[1]}")
print(f"RECEIVED {net_network_trade_tokens[2]} TOKEN-2 = ${net_network_trade_value[2]}")
print(f"RECEIVED {net_network_trade_tokens[3]} TOKEN-3 = ${net_network_trade_value[3]}")
print(f"\nSUM OF RECEIVED TOKENS USD VALUE = ${sum(net_network_trade_value)}")
print(f"CONVEX OPTIMISATION SOLVER RESULT: ${prob.value}\n")
这是定义交易代码的输出、它们的执行顺序、启动交易所需的最小 token 数量以及从套利中收到的 token 总数。
arbitrage.py的输出
我希望你已经学到了一些新东西,并在套利工具包中添加了一个新工具。
下次再见。
noxx